惯性主矩 应用哈默纳科执行元件FHA-17C-100-E250-C

 惯性主矩 应用哈默纳科执行元件FHA-17C-100-E250-C惯性矩是一个物理量，通常被用作描述一个物体抵抗弯曲的能力。惯性矩的国际单位为(m^4)。

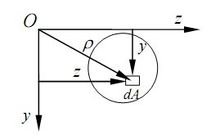面积元素dA与其至z轴或y轴距离平方的乘积y^2dA或z^2dA，分别称为该面积元素对于z轴或y轴的惯性矩或截面二次轴矩。

对Z轴的惯性矩：IZ=∫y^2dA（积分式如左图)对Y轴的惯性矩：

Iy=∫z^2dA

截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩。

 惯性主矩 应用哈默纳科执行元件FHA-17C-100-E250-C极惯性矩常用计算公式：Ip=∫ρ^2dA

矩形对于中线(垂直于h边的中轴线)的惯性矩：b*h^3/12

三角形：b*h^3/36

圆形对于圆心的惯性矩：π*d^4/64

环形对于圆心的惯性矩：π*D^4*（1-α^4)/64;α=d/D

d^4表示d的4次方。

需要明确因为坐标系不同计算公式也不尽相同。